Универсальный метод решения задач ЛП называется симплекс-методом. Применение этого метода и его наиболее часто встречающейся модификации - двухфазного симплекс-метода мы поясним на примерах.
Пример . Решить следующую задачу ЛП в канонической форме симплекс-методом. (5.5) (5.6)
x i ≥ 0, i = 1,…,6 (5.7)
Говорят, что задача ЛП имеет каноническую форму, если все ограничения (кроме условий неотрицательности переменных) имеют вид равенств, а все свободные члены неотрицательны. Так что мы имеем задачу в канонической форме.
Идея симплекс-метода заключается в следующем. Сначала нужно найти некоторую (начальную) вершину многогранника допустимых решений (начальное допустимое базисное решение). Затем нужно проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность. Ввиду конечности вершин многогранника (следствие конечности ограничений задачи ЛП) за конечное число "шагов" мы найдем искомую точку минимума или максимума. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум).
Таким образом, идея симплекс-метода основывается на трех свойствах задачи ЛП.
Решение. Чтобы найти начальное допустимое базисное решение, т.е. чтобы определить базисные переменные, систему (5.6) нужно привести к "диагональному" виду. Применяя метод Гаусса (метод последовательного исключения неизвестных), получаем из (5.6): (5.8)
Следовательно, базисными являются переменные x 2 , x 4 , x 5 , x 6 , им придаем значения, равные свободным членам соответствующих строк: x 2 =40, x 4 =20, x 5 =10, x 6 =30, . Переменные x 1 и x 3 являются небазисными: x 1 =0, x 3 =0 .
Построим начальное допустимое базисное решение
x 0 = (0,40,0,20,10,30) (5.9)
Для проверки на оптимальность найденного решения x 0 нужно из целевой функции исключить базисные переменные (с помощью системы (5.8)) и построить специальную симплекс таблицу.
После исключения переменных целевую функцию удобно записать в виде:
f(x) = -7x 1 – 14x 3 +880 (5.10)
Теперь при помощи (5.8) –(5.10) составляем начальную симплекс-таблицу:

В нулевую строчку записаны коэффициенты с обратным знаком соответствующих переменных при целевой функции. Критерий оптимальности (для задачи на поиск минимума): допустимое базисное решение(x 0 ) оптимально, если в нулевой строчке нет ни одного строго положительного числа (не считая значения целевой функции (880)). Это правило распространяется и на следующие итерации (таблицы). Элементы нулевой строки будем называть оценками столбцов.
Так что начальное допустимое базисное решение (5.9) неоптимально: 7>0, 14>0 .
В нулевом столбике записаны значения базисных переменных. Они обязательно должны быть неотрицательными (см. уравнение (5.7)). От первой по четвертую строки написаны коэффициенты переменных из системы (5.8).
Так как x 0 неоптимально, то надо перейти к другой вершине многогранника допустимых решений (построить новое д.б.р.). Для этого нужно найти ведущий элемент и провести определенное преобразование (симплексное преобразование).
Сначала находим ведущий элемент таблицы, который стоит в пересечении ведущего столбика (столбец с наибольшей положительной оценкой) и ведущей строки (строки, соответствующей минимальному соотношению элементов нулевого столбика к соответствующим элементам (строго положительным) ведущего столбика).
В таблице 1 ведущий столбик - третий столбик, и ведущая строка - четвертая строка (min{40/1,30/1}=30/1) обозначены стрелками, а ведущий элемент - кружочком. Ведущий элемент показывает, что базисную переменную x 6 нужно заменить на небазисную x 3 . Тогда новыми базисными переменными будут x 2 , x 3 , x 4 , x 5 , , а небазисными -x 1 , x 6 , . Это и означает переход к новой вершине многогранника допустимых решений. Чтобы найти значения координат нового допустимого базисного решения x 00 нужно строить новую симплекс-таблицу и провести в ней элементарные преобразования:
а) все элементы ведущей строки поделить на ведущий элемент, превратив этим самым ведущий элемент в 1 (для простоты выкладок);
б) с помощью ведущего элемента (равного 1) все элементы ведущего столбика превратить в нули (аналогично методу исключения неизвестных);
В результате в нулевом столбце получены значения новых базисных переменных x 2 , x 3 , x 4 , x 5 , (см. таблицу 2) - базисные компоненты новой вершины x 00 (небазисные компоненты x 1 =0, x 6 =0, ).

Как показывает таблица 2, новое базисное решение x 00 =(0,10,30,20,40,0) неоптимально (в нулевой строке есть неотрицательная оценка 7). Поэтому с ведущим элементом 1 (см. таблицу 2) строим новую симплекс-таблицу, т.е. строим новое допустимое базисное решение

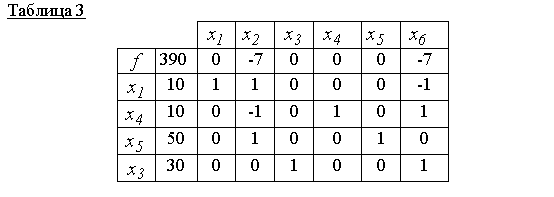
Таблице 3 соответствует допустимое базисное решение x 000 =(10,0,30,10,50,0) и оно оптимально, т.к. в нулевой строчке нет положительных оценок. Поэтому f(x 000)=390 есть минимальное значение целевой функции.
Ответ: x 000 =(10, 0, 30, 10, 50, 0) - точка минимума, f(x 000)=390 .

Рассмотрим универсальный метод решения канонической задачи линейного программирования

с n переменными и m ограничениями-равенствами, известный как симплекс-метод.

Множество планов канонической задачи - выпуклое многогранное множество, имеющее конечное число угловых точек. И если эта задача имеет оптимальное решение, то оно достигается хотя бы в одной угловой точке.

С любой угловой точкой связан базисный план задачи, в котором переменных равны нулю, а оставшимся переменным соответствуют линейно независимые столбцы матрицы условий. Эти линейно независимые столбцы образуют невырожденную базисную матрицу.

Перебор всех угловых точек сопряжен с большими вычислительными затратами и поэтому не эффективен. В 1947 году Дж. Данциг предложил упорядоченную процедуру перебора угловых точек, при которой для нахождения оптимального решения достаточно исследовать лишь небольшую их часть. Эта процедура называется симплекс-методом .

Дж. Данциг предложил при переходе от одной крайней точки к другой заменять в базисной матрице всего один вектор. Это означает, что при таком переходе мы должны одну из базисных переменных исключить - сделать ее небазисной (равной нулю), а на ее место ввести новую переменную из числа небазисных (нулевых) - сделать ее базисной (положительной).

Оказывается, геометрически такая замена приводит к переходу от одной угловой точки к смежной (соседней), связанной с предыдущей точкой общим ребром.

Из всех соседних точек выбирается та, в которой целевая функция возрастает более всего. Поскольку число угловых точек конечно, через конечное число переходов будет найдена вершина с наибольшим значением целевой функции, либо будет установлена неограниченность целевой функции на неограниченном множестве планов.

Общая схема симплекс-метода состоит из следующих основных шагов.

· шаг 0 . Определение начального базиса и соответствующей ему начальной угловой точки (базисного плана) .

· шаг 1 . Проверка текущего базисного плана на оптимальность. Если критерий оптимальности выполнен, то план оптимален и решение закончено. Иначе переход на шаг 2.

· шаг 2 . Нахождение переменной, вводимой в состав базисных. (Из условия увеличения целевой функции).

· шаг 3 . Нахождение переменной, исключаемой из состава базисных переменных (Из условия сохранения ограничений задачи).

· шаг 4 . Нахождение координат нового базисного плана (смежной угловой точки). Переход на шаг 1.

Повторяющиеся шаги 1-4 образуют одну итерацию симплекс-метода.

Из этой схемы следует, что во-первых, для начала работы симплекс-метода надо иметь какую-то угловую точку - начальный базисный план, а во-вторых, надо уметь исследовать текущую угловую точку на оптимальность, не вычисляя всех смежных вершин. Эти проблемы легко решаются, если каноническая задача ЛП имеет некий специальный вид.

Определение . Будем говорить, что каноническая задача ЛП имеет "предпочтительный вид", если

1. правые части уравнений, .

2. матрица условий содержит единичную подматрицу размера

Другими словами, в любом уравнении есть переменная с коэффициентом равным единице, отсутствующая в остальных уравнениях. Первое условие не является обременительным, так как в случае отрицательной правой части некоторого уравнения, достаточно умножить его на (-1). В задаче предпочтительного вида начальный базисный план находится очень просто.

Пример 2.1.

Матрица условий A и вектор правых частей ограничений b имеют вид

а целевой вектор с = (1, -3, 0, 4, 2).

Сразу очевидна одна базисная матрица: с единичными векторами условий.

Следовательно, выбирая в качестве базисных переменных x 1 , x 3 , x 5 , и полагая в системе уравнений x 2 = x 4 = 0 (небазисные переменные), немедленно находим x 1 = 10, x 3 = 20, x 5 = 8, так что начальный базисный план x 0 = (10, 0, 20, 0, 8). Видим, что значения базисных переменных равны правым частям ограничений. Из этого понятно требование положительности правых частей b i .

В дальнейшем, базисные переменные будем объединять в вектор x Б.

Таким образом, в канонической задаче предпочтительного вида в качестве начальной базисной матрицы берется единичная подматрица A Б = E , а соответствующие ей базисные переменные равны правым частям ограничений:

x Б = b .

Для базисного плана такого вида может быть сформулирован достаточно простой для проверки критерий оптимальности. Введем величины

? j = < с Б , A j > - c j , j = 1,...,n, (2.1)

где с Б - вектор из коэффициентов целевой функции при базисных переменных x Б , A j - j- й столбец матрицы условий, c j - j- й коэффициент целевой функции. Разности ? j называются симплексными разностями или симплексными оценками.

Критерий оптимальности базисного плана . Если для базисного плана с единичной базисной матрицей все симплексные оценки неотрицательны, то этот план оптимален.

Применим данный критерий для проверки на оптимальность базисного плана x 0 = (10, 0, 20, 0, 8) из примера 2.1.

Так как в этом плане вектор базисных переменных x Б =(x 1 , x 3 , x 5 ), то с Б = (c 1 , c 3 , c 5 ) = (1, 0, 2).

Следовательно,

? 1 = < с Б , A 1 > - c 1 = 1 1 + 0 0 + 2 0 - 1= 0,

2 = < сБ, A2 > - c2 = 1 3 + 0 1 + 2 2 - (-3) = 10,

? 3 = < с Б , A 3 > - c 3 = 1 0 + 0 1 + 2 0 - 0= 0,

? 4 = < с Б , A 4 > - c 4 = 1 (-1) + 0 5 + 2 1 - 4= -3,

? 5 = < с Б , A 5 > - c 5 = 1 0 + 0 0 + 2 1 - 2= 0.

Так как оценка ? 4 < 0, то базисный план x 0 не оптимален. Заметим, что симплексные оценки, соответствующие базисным переменным, всегда равны нулю, так что достаточно проверять только небазисные оценки.

Лекция 3. Симплексные таблицы. Алгоритм симплексного метода.

§ 3 СИМПЛЕКСНЫЙ МЕТОД

3.1. Общая идея симплекс–метода. Геометрическая интерпретация

Графический способ применим к весьма узкому классу задач линейного программирования: эффективно им можно решать задачи, содержащие не более двух переменных. Были рассмотрены основные теоремы линейного программи­рования, из которых следует, что если задача линейного програм­мирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает, по крайней мере, с одним из допустимых базисных решений систе­мы ограничений. Был указан путь решения любой задачи линейного программирования: перебрать конечное число допустимых базисных решений системы ограни­чений и выбрать среди них то, на котором функция цели прини­мает оптимальное решение. Геометрически это соответствует пе­ребору всех угловых точек многогранника решений. Такой пере­бор в конце концов приведет к оптимальному решению (если оно существует), однако его практическое осуществление связано с огромными трудностями, так как для реальных задач число допус­тимых базисных решений хотя и конечно, но может быть чрезвы­чайно велико.

Число перебираемых допустимых базисных решений можно сократить, если производить перебор не беспорядочно, а с учетом изменений линейной функции, т.е. добиваясь того, чтобы каждое следующее решение было "лучше" (или, по крайней мере, "не хуже"), чем предыдущее, по значениям линейной функции (увеличение ее при отыскании максимума , уменьшение– при отыскании минимума
). Такой перебор позволяет сократить число шагов при отыска­нии оптимума. Поясним это на графическом примере.

Пусть область допустимых решений изображается многоуголь­ником ABCDE . Предположим, что его угловая точка А соответствует исходному допустимому базисному решению. При беспорядочном переборе пришлось бы испытать пять допустимых базисных решений, соответствующих пяти угловым точкам мно­гоугольника. Однако из чертежа видно, что после вершины А выгодно перейти к соседней вершине В, а затем – к оптимальной точке С. Вместо пяти перебрали только три вершины, последовательно улучшая линейную функцию.

Идея последовательного улучшения решения легла в основу универсального метода решения задач линейного программирова­ния – симплексного метода или метода последовательного улучшения плана.

Геометрический смысл симплексного метода состоит в последо­вательном переходе от одной вершины многогранника ограничений (называемой первоначальной) к соседней, в которой линейная функция принимает лучшее (по крайней мере, не худшее) значение по отношению к цели задачи; до тех пор, пока не будет найдено оптимальное решение – вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум).

Впервые симплексный метод был предложен американским ученым Дж. Данцигом в 1949 г., однако еще в 1939 г. идеи метода были разработаны российским ученым Л.В. Канторовичем.

Симплексный метод, позволяющий решить любую задачу ли­нейного программирования, универсален. В настоящее время он используется для компьютерных расчетов, однако несложные при­меры с применением симплексного метода можно решать и вручную.

Для реализации симплексного метода – последовательного улучшения решения – необходимо освоить три основных элемента:

способ определения какого-либо первоначального допустимого базисного решения задачи;

правило перехода к лучшему (точнее, не худшему) решению;

критерий проверки оптимальности найденного решения.

Для использования симплексного метода задача линейного программирования должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена в виде урав­нений.

В литературе достаточно подробно описываются: нахождение начального опорного плана (первоначального допустимого базисного решения), тоже – методом искусственного базиса, нахождение оптимального опорного плана, решение задач с помощью симплексных таблиц.

3.2. Алгоритм симплекс–метода.

Рассмотрим решение ЗЛП симплекс-ме­тодом и изложим ее применительно к задаче максимизации.

1. По условию задачи составляется ее математическая мо­дель.

2. Составленная модель преобразовывается к канонической форме. При этом может выделиться базис с начальным опорным планом.

3. Каноническая модель задачи записывается в форме симп­лекс-таблицы так, чтобы все свободные члены были неотрицатель­ными. Если начальный опорный план выделен, то переходят к пункту 5.

Симплекс таблица: вписывается система ограничительных уравнений и целевая функция в виде выражений, разрешенных относительно начального базиса. Строку, в которую вписаны коэффициенты целевой функции
, называют
–строкой или строкой целевой функции.

4. Находят начальный опорный план, производя симплексные преобразования с положительными разрешающими элементами, отвечающими минимальным симплексным отношениям, и не при­нимая во внимание знаки элементов
–строки. Если в ходе преоб­разований встретится 0-строка, все элементы которой, кроме сво­бодного члена, нули, то система ограничительных уравнений задачи несовместна. Если же встретится 0-строка, в которой, кроме свободного члена, других положительных элементов нет, то систе­ма ограничительных уравнений не имеет неотрицательных ре­шений.

Приведение системы (2.55), (2.56) к новому базису будем на­зывать симплексным преобразованием . Если симплексное преобра­зование рассматривать как формальную алгебраическую операцию, то можно заметить, что в результате этой операции происходит перераспределение ролей между двумя переменными, входя­щими в некоторую систему линейных функций: одна переменная из зависимых переходит в независимые, а другая наоборот – из независимых в зависимые. Такая операция известна в алгебре под названием шага жорданова исключения.

5. Найденный начальный опорный план исследуется на опти­мальность:

а) если в
–строке нет отрицательных элементов (не считая свободного члена), то план оптимален. Если при этом нет и нуле­вых, то оптимальный план единственный; если же есть хотя бы один нулевой, то оптимальных планов бесконечное множество;

б) если в
–строке есть хотя бы один отрицательный элемент, которому соответствует столбец неположительных элементов, то
;

в) если в
–строке есть хотя бы один отрицательный элемент, а в его столбце есть хотя бы один положительный, то можно пе­рейти к новому опорному плану, более близкому к оптимальному. Для этого указанный столбец надо назначить разрешающим, по минимальному симплексному отношению найти разрешающую строку и выполнить симплексное преобразование. Полученный опорный план вновь исследовать на оптимальность. Описанный процесс повторяется до получения оптимального плана либо до установления неразрешимости задачи.

Столбец коэффициентов при переменной, включаемой в базис, называют разрешаю­щим. Таким образом, выбирая переменную, вводимую в базис (или выбирая разрешающий столбец) по отрицательному эле­менту
–строки, мы обеспечиваем возрастание функции
.

Немного сложней определяется переменная, подлежащая ис­ключению из базиса. Для этого составляют отношения свободных членов к положительным элементам разрешающего столбца (та­кие отношения называют симплексными) и находят среди них наименьшее, которое и определяет строку (разрешающую), содержащую исключаемую переменную. Выбор переменной, ис­ключаемой из базиса (или выбор разрешающей строки), по ми­нимальному симплексному отношению гарантирует, как уже уста­новлено, положительность базисных компонент в новом опорном плане.

В пункте 3 алгоритма предполагается, что все элементы столбца свободных членов неотрицательны. Это требование не обя­зательно, но если оно выполнено, то все последующие симплексные преобразования производятся только с положительными разре­шающими элементами, что удобно при расчетах. Если в столбце свободных членов есть отрицательные числа, то разрешающий элемент выбирают следующим образом:

1) просматривают строку, отвечающую какому-либо отрица­тельному свободному члену, например –строку, и выбирают в ней какой-либо отрицательный элемент, а соответствующий ему стол­бец принимают за разрешающий (предполагаем, что ограничения задачи совместны);

2) составляют отношения элементов столбца свободных чле­нов к соответствующим элементам разрешающего столбца, имею­щим одинаковые знаки (симплексные отношения);

3) из симплексных отношений выбирают наименьшее. Оно и определит разрешающую строку. Пусть ею будет, например, р –строка;

4) на пересечении разрешающих столбца и строки находят разрешающий элемент. Если разрешающим оказался элемент –строки, то после симплексного преобразования свободный член этой строки станет положительным. В противном случае на сле­дующем шаге вновь обращаются к–строке. Если задача разреши­ма, то через некоторое число шагов в столбце свободных членов не останется отрицательных элементов.

Если в форму ЗЛП облечена некоторая реальная производст­венная ситуация, то дополнительные переменные, которые прихо­дится вводить в модель в процессе преобразования ее к каноничес­кой форме, всегда имеют определенный экономический смысл.

Симплекс-метод

1. Идея симплекс-метода

Рассмотрим универсальный метод решения канонической задачи ЛП.

известный как симплекс-метод.

Как было установлено в главе 2, множество планов канонической задачи - выпуклое многогранное множество, имеющее конечное число угловых точек. И если эта задача имеет оптимальное решение, то оно достигается хотя бы в одной угловой точке.

С любой угловой точкой связан базисный план задачи, в котором переменных равны нулю, а оставшимся переменным соответствуют линейно независимые столбцы матрицы условий. Эти линейно независимые столбцы образуют невырожденную базисную матрицу.

Перебор всех угловых точек сопряжен с большими вычислительными затратами и поэтому не эффективен. В 1944 году Дж. Данциг предложил упорядоченную процедуру перебора угловых точек, при которой для нахождения оптимального решения достаточно исследовать лишь небольшую их часть. Эта процедура называется симплекс-методом.

Дж. Данциг предложил при переходе от одной крайней точки к другой заменять в базисной матрице всего один вектор. Это означает, что при таком переходе мы должны одну из базисных переменных исключить - сделать ее небазисной (равной нулю), а на ее место ввести новую переменную из числа небазисных (нулевых) - сделать ее базисной (положительной).

Оказывается, геометрически такая замена приводит к переходу от одной угловой точки к смежной (соседней), связанной с предыдущей точкой общим ребром.

Из всех соседних точек выбирается та, в которой целевая функция возрастает более всего. Поскольку число угловых точек конечно, через конечное число переходов будет найдена вершина с наибольшим значением целевой функции, либо будет установлена неограниченность целевой функции на неограниченном множестве планов.

Общая схема симплекс-метода состоит из следующих основных шагов.

·0 шаг . Определение начального базиса и соответствующей ему начальной угловой точки (базисного плана) .

·1 шаг . Проверка текущего базисного плана на оптимальность. Если критерий оптимальности выполнен, то план оптимален и решение закончено. Иначе переход на шаг 2.

·2 шаг . Нахождение переменной, вводимой в состав базисных. (Из условия увеличения целевой функции).

·3 шаг . Нахождение переменной, исключаемой из состава базисных переменных (Из условия сохранения ограничений задачи).

·4 шаг . Нахождение координат нового базисного плана (смежной угловой точки). Переход на шаг 1.

Повторяющиеся шаги 1-4 образуют одну итерацию симплекс-метода.

Из этой схемы следует, что, во-первых, для начала работы симплекс-метода надо иметь какую-то угловую точку - начальный базисный план, а во-вторых, надо уметь исследовать текущую угловую точку на оптимальность, не вычисляя всех смежных вершин. Эти проблемы легко решаются, если каноническая задача ЛП имеет некий специальный вид.

Определение . Будем говорить, что каноническая задача ЛП имеет «предпочтительный вид», если

1.правые части уравнений, .

Матрица условий содержит единичную подматрицу размера

Другими словами, в любом уравнении есть переменная с коэффициентом равным единице, отсутствующая в остальных уравнениях. Условие 1 не является обременительным, так как в случае отрицательной правой части некоторого уравнения, достаточно умножить его на (-1). В задаче предпочтительного вида начальный базисный план находится очень просто.

Пример.

Матрица условий и вектор правых частей ограничений имеют вид

Сразу очевидна одна базисная матрица: с единичными векторами

Следовательно, - базисные переменные, а x2, x4 - небазисные. Полагая в системе уравнений x2=x4 =0, немедленно находим x1 =10, x3 =20, x5 =8. Видим, что значения базисных переменных равны правым частям ограничений. Из этого понятно требование положительности правых частей bi.

В дальнейшем, базисные переменные будем объединять в вектор x Б.

Таким образом, в канонической задаче предпочтительного вида в качестве начальной базисной матрицы берется единичная подматрица AБ =E, а соответствующие ей базисные переменные равны правым частям ограничений: xБ =b.

. Простейшая реализация симплекс-метода

Простейшая реализация симплекс-метода («простой С-метод») применяется к канонической задаче ЛП, имеющей «предпочтительный вид». Не умаляя общности, будем считать, что единичная подматрица содержится в первых m столбцах. Тогда каноническая задача запишется следующим образом

f(x) = c1x1 + c2x2 +… + cmxm + cm+1xm+1 +… + cnxn ??max(3.1)x1 + a1m+1 xm+1 + … + a1n xn = b1(3.2)x2 + a2m+1 xm+1 + … + a2n xn = b2………………………………………………………….xm + amm+1 xm+1 + … + amn xn = bmxj³ 0, j=1,2,…, n.(3.3)

Матрица условий

содержит единичную подматрицу размера m x m в первых m столбцах, следовательно AБ ={A1, A2,…, Am}=E.

Основные шаги симплекс-метода (теория)

Поскольку единичная базисная матрица находится в первых m столбцах матрицы условий, то первые m координат начального базисного плана являются базисными, а последние n - m координат являются небазисными, то есть равны нулю:

o = (x1, x2,…, xm, 0,…, 0).

Подставляя координаты точки xo в ограничения (3.2) и учитывая, чтоm+1 =… = xn = 0, получаем: x1 = b1, x2 = b2,…, xm = bm, то есть xoБ = b.

Значит начальный базисный план имеет вид:

xo = (b1,…, bm, 0,…, 0),

где сБ = (с1,…, сm) - вектор, составленный из коэффициентов целевой функции при базисных переменных.

1 шаг.

Из системы ограничений (3.2) выразим базисные переменные через небазисные:

x1= b1 - a1m+1xm+1 - … - a1nxn, x2 = b2 - a2m+1xm+1 - … - a2nxn, ………………………………………… xm = bm - amm+1xm+1 - … - amnxn,(3.4)

Подставим эти выражения в целевую функцию (3.1).

f (x) = c1 (b1 - a1m+1xm+1 - … - a1nxn) + c2 (b2 - a2m+1xm+1 - … - a2nxn) +

………………………………………………..

Cm (bm - amm+1xm+1 - … - amnxn) + cm+1xm+1 +… + cnxn.

Сгруппируем слагаемые при одинаковых небазисных переменных:

f (x) = - (c1 a1m+1 + c2 a2m+1 + … + cm amm+1 - cm+1).xm+1 - …-

- (c1 a1n + c2 a2n + … + cm amn - cn). xn.(3.5)

Заметим, что выражения в круглых скобках можно записать в виде

c1 a1m+1 + c2 a2m+1 + … + cm amm+1 - cm+1 = < cБ, Am+1 > - cm+1 = Dm+1,

…………………………………………………………………………………………………………………………1 a1n + c2 a2n + … + cm amn - cn = < cБ, An > - cn = Dn,

где сБ = (с1,…, сm) - вектор, составленный из коэффициентов целевой функции при базисных переменных, Am+1,…, An - столбцы матрицы условий А при небазисных переменных xm+1,…, xn.

Выражения

D j = < сБ, Aj > - cj, j = m+1,…, n,(3.6)

называются симплексными разностями или симплексными оценками базисного плана.

С учетом (3.6), формулу (3.5) для целевой функции можно переписать в виде

Эта формула позволяет получить признак оптимальности базисного плана. Если все симплексные оценки с небазисными номерами D j ³ 0, то текущий базисный план - оптимален.

Действительно, если хотя бы одна оценка, например, ?k строго отрицательна, то придавая соответствующей небазисной переменной xk положительное значение, а остальные небазисные переменные плана x полагая равными нулю, получим

f (x) = f (xo) - Dk xk = f (xo) + | D k | xk > f (xo),(3.7)

то есть в этом случае план xo может быть улучшен.

Легко проверить, что симплексные оценки, соответствующие единичным базисным столбцам всегда равны 0.

2 шаг . Нахождение переменной вводимой в состав базисных переменных.

Как следует из формулы (3.7), целевую функцию можно увеличить, если ввести в состав базисных переменных (сделать положительной) небазисную переменную xj, которой соответствует отрицательная оценка?j < 0. Если таких оценок несколько, то обычно в состав базисных вводят небазисную переменную хк с наибольшей по модулю отрицательной оценкой, то есть такую, для которой

где D j = < CБ, Aj > - cj, j = m+1,…, n (номера небазисных переменных).

Таким образом мы получим новый план

x1 = (x1,…, xm,0,…, xk,…, 0,…, 0).

Но х1 - небазисный план, так как число положительных координат равно m+1, число нулевых координат равно n - m -1.

Чтобы получить новую угловую точку, занулим одну из базисных переменных, то есть выведем одну переменную из состава базисных.

3 шаг.

Подставим координаты точки х1 в условия (3.4) и учтем, что переменные xj должны быть неотрицательны

x1 = b1 - a1kxk³ 0 x2 = b2 - a2kxk³ 0 …………………………. xm = bm - amkxk³ 0(3.8)

Из формулы (3.7) видно, что чем больше величина хк > 0, тем больше возрастает целевая функция. Постараемся найти максимальное значение хк, не нарушая ограничений задачи и выполняя условия неотрицательности (3.8).

Неравенства (3.8) можно переписать в виде

A1kxk£ b1 a2kxk£ b2 ……………… amkxk £ bm(3.9)

При решении системы неравенств (3.9) возможны два случая:) среди коэффициентов при хк нет положительных: aik£ 0, i=1,2,…, m. Так как bi> 0, то неравенства (3.9) выполняются при любом сколь угодно большом значении хк. Это говорит о том, что целевая функция не ограничена на множестве планов (max f(x) ® ¥) и следовательно, решения задачи ЛП не существует.) среди коэффициентов при хк есть положительные aik > 0. Решая систему неравенств (3.9) получим:

хк £ bi /aik, для всех i, для которых aik > 0.(3.10)

Наибольшее значение хк, удовлетворяющее всем ограничениям (3.10), равно наименьшему из отношений в правых частях этих неравенств

хк = min {bi /aik} по всем i: aik > 0.

Пусть минимум достигается при i = r, то есть хк ? br /ark. Это означает, что базисная переменная хr в условиях (3.8) обращается в нуль.

хr = br - ark xk = br - ark (br /ark) = 0, 1 ??r ??m.

Переменная xr исключается из базиса. Следовательно, получили новый состав базисных и небазисных переменных, отличающийся от исходного одной базисной и одной небазисной координатой.

4 шаг.

Новый базисный план будет иметь вид

1 = (x1, x2,…, 0,…, xm, 0,…, хk,0,…, 0),

где на месте хr стоит ноль, а хк > 0.тому базисному плану соответствует новая базисная матрица:

Для нахождения координат новой угловой точки х1 каноническая задача ЛП приводится к новому предпочтительному виду, то есть к такой форме, чтобы матрица стала единичной (= E). Для этого столбец Аk нужно преобразовать к единичному представлению,

R-я строка,

в котором коэффициент = 1, а все остальные элементы =0, i ??r. Этого можно добиться с помощью элементарных операций над уравнениями системы. Решение заканчивается тогда, когда для некоторой точки все оценки Dj ³ 0.

3. Реализация симплекс-метода на примере

Продемонстрируем применение симплекс-метода на примере из главы 2.

Рассмотрим каноническую задачу ЛП

f(x) = x1+ 2x2 +0 x3 + 0 x4 max(3.11)-x1+ 2x2+ x3 = 4,(3.12)3 x1 +2x2 + x4 = 12,(3.13)xj ? 0, j = 1,2,3,4.(3.14)

Матрица условий A = (A1, A2, A3, A4), где

Целевой вектор c =(c1, c2, c3, c4)=(1, 2, 0, 0); вектор правых частей b=(b1, b2) = (4, 12).

0 шаг. Нахождение начальной угловой точки (базисного плана).

Задача имеет предпочтительный вид, так как правые части уравнений положительны, а столбцы матрицы условий A3, A4 образуют единичную подматрицу. Значит начальная базисная матрица = (A3, A4); x3 и x4 - базисные переменные, x1 и x2 - небазисные переменные, cБ = (c3, c4) = (0, 0).

Начальный базисный план имеет вид

x0 = (0, 0, x3, x4) = (0, 0, 4, 12); f(xo) = 0.

1 шаг. Проверка базисного плана на оптимальность.

Подсчитаем симплексные оценки для небазисных переменных по формуле (3.6)

D1 = < cБ, A1 > - c1 = 0 ·(-1) + 0 ·3 - 1 = -1.

D2 = < cБ, A2 > - c2 = 0 ·2 + 0 · 2 - 2 = -2.

Так как оценки отрицательны, то план xo - не оптимален. Будем искать новый базисный план (смежную угловую точку) с большим значением целевой функции.

2 шаг . Нахождение переменной вводимой в базис.

Целевую функцию можно увеличить, если ввести в состав базисных переменных (сделать положительной) одну из небазисных переменных x1 или x2, поскольку обе оценки Dj < 0. Обычно в состав базисных вводят небазисную переменную с наибольшей по модулю отрицательной оценкой, поэтому будем вводить в базис переменную x2.

3 шаг. Определение переменной выводимой из базиса.

После ввода в базис переменной x2 новый план будет иметь вид1 = (0, x2, x3, x4).

Этот план не является базисным, так как он содержит только одну нулевую координату, значит надо сделать нулевой (исключить из базиса) одну из переменных x3 или x4.

Подставим координаты плана x1 = (0, x2, x3, x4) в ограничения задачи. Получим

Выразим отсюда базисные переменные x3 и x4 через переменную x2, вводимую в базис.

x3 = 4 - 2x2,(3.15)x4 = 12 - 2x2.(3.16)

Так переменные x3 и x4 должны быть неотрицательны, получим систему неравенств

4 - 2x2 ³ 0,(3.17)12 - 2x2 ³ 0.(3.18)

Чем больше значение x2, тем больше возрастает целевая функция. Найдем максимальное значение новой базисной переменной, не нарушающее ограничения задачи, то есть удовлетворяющее условиям (3.17), (3.18).

Перепишем неравенства в виде

x2£ 4,

x2£12,

откуда максимальное значение x2 = min {4/2, 12/2} = 2. Подставляя это значение в выражения (3.15), (3.16) для x3 и x4, получаем x3 = 0. Следовательно x3 выводится из базиса.

4 шаг. Определение координат нового базисного плана.

Новый базисный план (смежная угловая точка) имеет вид

x1 = (0, x2, 0, x4).

Базис этой точки состоит из столбцов A2 и A4, так что = (A2, A4). Заметим, что этот базис не является единичным, так как вектор A2 = (2, 2), и следовательно задача (3.11) - (3.14) не имеет предпочтительного вида относительно нового базиса. Преобразуем условия задачи (3.12), (3.13) таким образом, чтобы она приняла предпочтительный вид относительно новых базисных переменных x2, x4, то есть чтобы переменная x2 входила в первое уравнение с коэффициентом, равным единице, и не присутствовала во втором уравнении. Перепишем уравнения задачи

x1+ 2x2+ x3 = 4, (p1)

x1 +2x2 + x4 = 12. (p2)

Поделим первое уравнение на коэффициент при x2. Получим новое уравнение = p1 / 2, эквивалентное исходному

1/2 x1+ x2+ 1/2 x3 = 2. ()

Используем это уравнение, которое назовем разрешающим, для исключения переменной x2 из второго уравнения. Для этого надо уравнение умножить на 2 и вычесть из p2. Получим уравнение = p2 - 2 = p2 - p1.

x1 - x3 + x4 = 8. ()

В итоге получили новое «предпочтительное» представление исходной задачи (3.11) - (3.14) относительно новых базисных переменных x2, x4:

f(x) = x1+ 2x2 + 0 x3 + 0 x4® max

1/2 x1+ x2+ 1/2 x3 = 2. ()

x1 - x3 + x4 = 8. ()

xj ³ 0, j = 1,2,3,4.

Подставляя сюда представление нового базисного плана x1 = (0, x2,0, x4), сразу найдем его координаты, так как значения базисных переменных равны правым частям уравнений

x1 = (0,2,0,8); f(x1)=4.

На этом завершается первая итерация простого симплекс-метода. Далее процесс решения задачи продолжается с шага 1, состоящем в проверке найденного плана на оптимальность. Решение заканчивается тогда, когда все симплексные оценки текущего базисного плана окажутся неотрицательными.

Мы не будем проводить вторую итерацию по схеме первой, поскольку все вычисления симплекс-метода удобнее проводить в табличном виде.

симплекс переменная канонический программирование

Литература

1. Эконометрика: Учебник / Под ред. И.И. Елисеевой. - М.: Финансы и статистика, 2002. - 344 с.: ил.

Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. - М.: Финансы и статистика, 2002. - 192 с.: ил.

Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов. - М.: ЮНИТИ-ДАНА, 2002. - 311 с.

Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: учебник. - М.: Дело, 2001. - 400 с.

Катышев П.К., Магнус Я.Р., Пересецкий А.А. Сборник задач к начальному курсу эконометрики. - 3-е изд., испр. - М.: Дело, 2003. - 208 с.

Доугерти К. Введение в эконометрику. - М.: Финансы и статистика, 1999.

Джонстон Дж. Эконометрические методы. - М.: Статистика, 1980.

Кейн Э. Экономическая статистика и эконометрия. Введение в количественный экономический анализ. Вып. 1. - М.: Статистика, 1977.

Ланге О. Введение в эконометрику / Пер. с польск. - М.: Прогресс, 1964.

Лизер С. Эконометрические методы и задачи. - М.: Статистика, 1971.

Маленво Э. Статистические методы эконометрии. - М.: Статистика, 1976.

Тинтнер Г. Введение в эконометрию. - М.: Финансы и статистика, 1965.

Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики: учебник для вузов. - М.: ЮНИТИ, 1998.

Вентцель Е.С. Теория вероятностей: Учебник для вузов. - 6-е изд. - М.: Высш. шк., 1999.

Идея симплекс– метода

Симплекс– метод

В предыдущем разделе было показано, что если задача линейного программирования имеет оптимальное решение, то одним из оптимальных решений является допустимое базисное решение ее системы ограничений, которое соответствует некоторой угловой точке многогранника допустимых решений системы. Было показано, как с помощью конечного перебора базисных решений системы ограничений задачи, найти это оптимальное решение. Однако с ростом размерности n системы ограничений задачи объем вычислений решения задачи методом полного перебора базисных решений растет экспоненциально и становится непригодным на практике. Можно организовать перебор только допустимых базисных решений и число перебираемых решений резко сократить, если каждое следующее допустимое базисное решение выбирать так, чтобы соответствующее значение целевой функции улучшалось или хотя бы не ухудшалось. Такой подход позволяет сократить число шагов при отыскании оптимального базисного решения. Эту идею поясним графически.

Пусть многоугольник ABCDEFGH изображает множество допустимых решений ЗЛП с двумя переменными, а вектор – градиент целевой функции.

Нужно найти точку этого многоугольника, в которой целевая функция принимает наименьшее значение. Пусть определено начальное допустимое базисное решение задачи, соответствующее угловой точке B. При полном переборе всех допустимых базисных решений придется исследовать восемь таких решений, соответствующих восьми угловым точкам многоугольника. Однако из рисунка видно, что, учитывая направление градиента , выгоднее перейти к соседней вершине C, затем к соседней вершине D, которой соответствует оптимальное базисное решение задачи. Таким образом, вместо восьми решений придется перебрать только три допустимых базисных решения.

Идея последовательного улучшения решения и положена в основу универсального метода решения задач линейного программирования – симплекс–метода.

Геометрический смысл симплекс–метода состоит в том, что выполняется последовательный переход от одной вершины многогранника допустимых решений задачи к соседней, в которой целевая функция принимает значение не худшее, чем в предыдущей вершине. Этот переход продолжается до тех пор, пока не будет найдено оптимальное решение или не будет обнаружено, что задача его не имеет.

Впервые симплекс–метод и его название были предложены американским математиком Джоном Данцигом в 1947 году, хотя идеи метода были опубликованы российским математиком Л.В. Канторовичем еще в 1939 году в статье «Математические методы организации и планирования производства».

Симплекс–метод состоит из трех основных элементов.